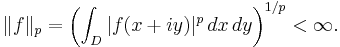Bergman space

In complex analysis, a branch of mathematics, a Bergman space, named after Stefan Bergman, is a function space of holomorphic functions in a domain D of the complex plane that are sufficiently well-behaved at the boundary that they are absolutely integrable. Specifically, 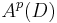$A^p(D)$ is the space of holomorphic functions in D such that the p-norm

$\|f\|_p = \left(\int_D |f(x%2Biy)|^p\,dx\,dy\right)^{1/p} < \infty.$

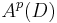Thus $A^p(D)$ is the subspace of homolorphic functions that are in the space L^p(D). The Bergman spaces are Banach spaces, which is a consequence of the estimate, valid on compact subsets K of D:

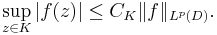
$\sup_{z\in K} |f(z)| \le C_K\|f\|_{L^p(D)}.$

(1)

Thus convergence of a sequence of holomorphic functions in L^p(D) implies also compact convergence, and so the limit function is also holomorphic.

If p = 2, then 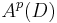$A^p(D)$ is a reproducing kernel Hilbert space, whose kernel is given by the Bergman kernel.

References

Richter, Stefan (2001), "Bergman spaces", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b120130 .

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›